双指针

1 算法解释

双指针顾名思义，就是同时使用两个指针，在序列、链表结构上指向的是位置，在树、图结构中指向的是节点，通过同向或相向移动来维护、统计信息。

双指针主要用于遍历数组，两个指针指向不同的元素，从而协同完成任务。也可以延伸到多个数组的多个指针。

若两个指针指向同一数组，遍历方向相同且不会相交，则也称为滑动窗口（两个指针包围的区域即为当前的窗口），经常用于区间搜索。

若两个指针指向同一数组，但是遍历方向相反，则可以用来进行搜索，待搜索的数组往往是排好序的。

2 题型分类

2.1 Two Sum

2.1.1 模板题——167. 两数之和 II - 输入有序数组

在一个增序的整数数组里找到两个数，使它们的和为给定值。已知有且只有一对解。

2.1.2 输入输出样例

输入是一个数组（numbers）和一个给定值（target）。输出是两个数的位置，从 1 开始计数。

Input: numbers = [2,7,11,15], target = 9
Output: [1,2]

在这个样例中，第一个数字（2）和第二个数字（7）的和等于给定值（9）。

2.1.3 题解

因为数组已经排好序，我们可以采用方向相反的双指针来寻找这两个数字，一个初始指向最小的元素，即数组最左边，向右遍历；一个初始指向最大的元素，即数组最右边，向左遍历。

如果两个指针指向元素的和等于给定值，那么它们就是我们要的结果。如果两个指针指向元素的和小于给定值，我们把左边的指针右移一位，使得当前的和增加一点。如果两个指针指向元素的和大于给定值，我们把右边的指针左移一位，使得当前的和减少一点。

vector<int> twoSum(vector<int>& numbers, int target) {
    int l = 0, r = numbers.size() - 1, sum;
    while (l < r) {
        sum = numbers[l] + numbers[r]; 
        if (sum > target) {
            r--;
        } else if (sum == target) {
            break;
        } else {
            l++;
        }
    }
    return vector<int> {l + 1, r + 1};
}

2.2 归并两个有序数组

2.2.1 模板题——88. 合并两个有序数组

给定两个有序数组，把两个数组合并为一个。

2.2.2 输入输出样例

输入是两个数组和它们分别的长度 m 和 n。其中第一个数组的长度被延长至 m + n，多出的 n 位被 0 填补。题目要求把第二个数组归并到第一个数组上，不需要开辟额外空间。

Input: nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
Output: nums1 = [1,2,2,3,5,6]

2.2.3 题解

因为这两个数组已经排好序，我们可以把两个指针分别放在两个数组的末尾，即 nums1 的 m - 1 位和 nums2 的 n - 1 位。每次将较大的那个数字复制到 nums1 的后边，然后向前移动一位。因为我们也要定位 nums1 的末尾，所以我们还需要第三个指针，以便复制。

在以下的代码里，我们直接利用 m 和 n 当作两个数组的指针，再额外创立一个 pos 指针，起始位置为 m + n - 1。每次向前移动 m 或 n 的时候，也要向前移动 pos。这里需要注意，如果 nums1 的数字已经复制完，不要忘记把 nums2 的数字继续复制；如果 nums2 的数字已经复制完，剩余 nums1 的数字不需要改变，因为它们已经被排好序。

void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
    int pos = (m--) + (n--) - 1;
    while (m >= 0 && n >= 0) {
        nums1[pos--] = nums1[m] > nums2[n] ? nums1[m--] : nums2[n--];
    }
    while (n >= 0) {
        nums1[pos--] = nums2[n--];
    }
}

2.3 快慢指针

2.3.1 模板题——142. 环形链表 II

给定一个链表，如果有环路，找出环路的开始点。

2.3.2 输入输出样例

输入是一个链表，输出是链表的一个节点。如果没有环路，返回一个空指针。

如果没有特殊说明， LeetCode 采用如下的数据结构表示链表。

struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(nullptr) {}
};

2.3.3 题解

对于链表找环路的问题，有一个通用的解法——快慢指针（Floyd 判圈法） 。给定两个指针，分别命名为 slow 和 fast，起始位置在链表的开头。每次 fast 前进两步， slow 前进一步。如果 fast 可以走到尽头，那么说明没有环路；如果 fast 可以无限走下去，那么说明一定有环路，且一定存在一个时刻 slow 和 fast 相遇。当 slow 和 fast 第一次相遇时，我们将 fast 重新移动到链表开头，并让 slow 和 fast 每次都前进一步。当 slow 和 fast 第二次相遇时，相遇的节点即为环路的开始点。

证明：

• 慢指针入环第一圈没走完的时候就会和快指针相遇
• $a=c+(n-1)(b+c)a=c+(n−1)(b+c) $的等量关系，我们会发现：从相遇点到入环点的距离加上 n−1​ 圈的环长，恰好等于从链表头部到入环点的距离。

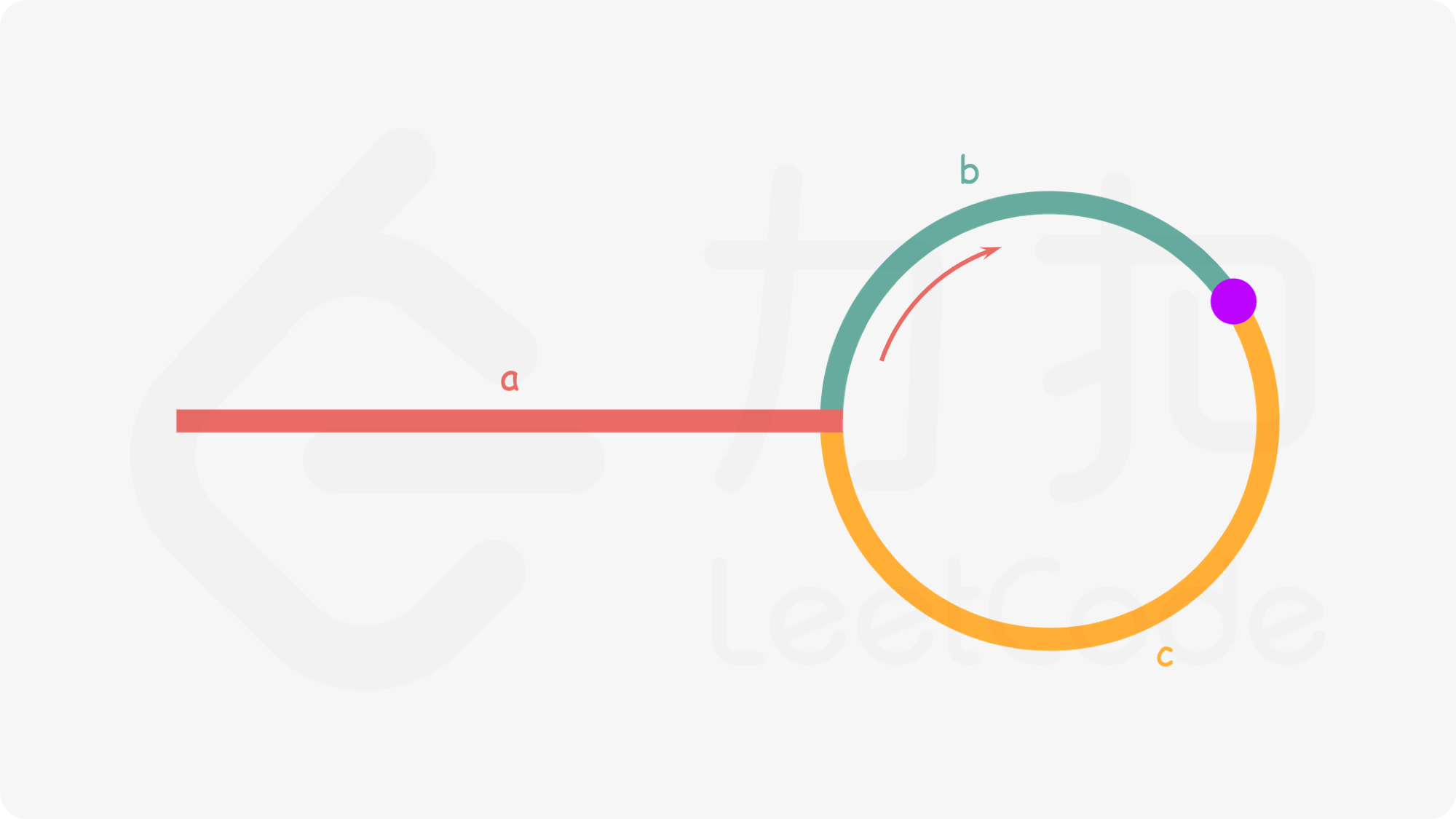
ListNode *detectCycle(ListNode *head) {
    ListNode *fast = head, *slow = head;
    // 判断是否存在环路
    do {
        if (!fast || !fast->next)
            return nullptr;
        fast = fast->next->next;
        slow = slow->next;
    } while (fast != slow);
    // 如果存在，查找环路节点
    fast = head;
    while (fast != slow) {
        slow = slow->next;
        fast = fast->next;
    }
    return fast;
}

2.4 滑动窗口

2.4.1 模板题——76. 最小覆盖子串

给定两个字符串 S 和 T，求 S 中包含 T 所有字符的最短连续子字符串的长度，同时要求时间复杂度不得超过 $O(n)$​。

2.4.2 输入输出样例

输入是两个字符串 S 和 T，输出是一个 S 字符串的子串。

Input: S = "ADOBECODEBANC", T = "ABC"
Output: "BANC"

在这个样例中， S 中同时包含一个 A、一个 B、一个 C 的最短子字符串是“BANC”。

2.4.3 题解

本题使用滑动窗口求解，即两个指针 l 和 r 都是从最左端向最右端移动，且 l 的位置一定在 r 的左边或重合。我们在 s 上滑动窗口，通过移动 r 指针不断扩张窗口。当窗口包含 t 全部所需的字符后，如果能收缩，我们就收缩窗口直到得到最小窗口。

注意本题虽然在 for 循环里出现了一个 while 循环，但是因为 while 循环负责移动 l 指针，且 l 只会从左到右移动一次，因此总时间复杂度仍然是 $O(n)$。本题使用了长度为 128 的数组来映射字符，也可以用哈希表替代；其中chars 表示目前每个字符缺少的数量， flag 表示每个字符是否在 T 中存在。

string minWindow(string s, string t) {
    vector<int> chars(128, 0);
    vector<bool> flag(128, false);
    // 先统计T中的字符情况
    for (auto ch : t) {
        flag[ch] = true;
        ++chars[ch];
    }
    // 移动滑动窗口， 不断更改统计数据
    int slen = s.size();
    int tlen = t.size();
    int cnt = 0, l = 0, min_l = 0, min_size = slen + 1;
    for (int r =0; r < slen; ++r) {
        if (flag[s[r]]) {
            if (--chars[s[r]] >= 0) {
                ++cnt;
            }
            // 若目前滑动窗口已包含T中全部字符，
            // 则尝试将l右移， 在不影响结果的情况下获得最短子字符串
            while (cnt == tlen) {
                if (r - l + 1 < min_size) {
                    min_l = l;
                    min_size = r - l + 1;
                }
                if (flag[s[l]] && ++chars[s[l]] > 0) {
                    --cnt;
                }
                ++l;
            }
        }
    }
    return min_size > slen ? "" : s.substr(min_l, min_size);
}

3 注意

4 参考

• OI-wiki

5 题目列表

需要配合OI-wiki刷题

试题链接	解题链接	备注
167. 两数之和 II - 输入有序数组	-	Two Sum模板
88. 合并两个有序数组	-	模板题目
142. 环形链表 II	-	模板题目
76. 最小覆盖子串	-	模板题目
633. 平方数之和	-	Two Sum变形，用long long
680. 验证回文字符串 Ⅱ	-	Two Sum变形，只允许一次失误，可以选择从左或右边跳过

---

1 无重复字符的最长子串

题目来源：leetcode-3 无重复字符的最长子串

思路

首先区分子串与子序列：子串必须连续，子序列可以不连续。

两层循环$O(n^2)$不太行，减少重复查询，可以用双指针维护一个滑动窗口，同时用一个数组标记滑动窗口内出现的字符。

• 时间复杂度：$O(N)$，其中 $N$ 是字符串的长度。左指针和右指针分别会遍历整个字符串一次。
• 空间复杂度：$O(|\Sigma|)$，其中 $\Sigma$ 表示字符集（即字符串中可以出现的字符），$|\Sigma|$ 表示字符集的大小。在本题中没有明确说明字符集，因此可以默认为所有 ASCII 码在 $[0, 128)$ 内的字符，即 $|\Sigma| = 128$。

代码

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        const int maxn = 128;//字符范围
        int foot[maxn] = {0};//标记滑动窗口中已经有的字符
        int len = s.size();
        if (len == 0) {//空串
            return 0;
        }
        int start = 0, end = 0;//双指针维护窗口
        foot[s[start]] = 1;
        int ans = 1;
        while (start < len - 1) {
            end++;//后面的指针前进
            while (end < len) {
                if (foot[s[end]] == 0) {
                    foot[s[end]] = 1;
                    end++;
                } else {
                    break;
                }
            }
            end--;//后面的指针回退
            ans = max(ans, end - start + 1);
            foot[s[start]] = 0;//前面的指针前移
            start++;
        }
        return ans;
    }
};